Machine Learning in FEA: een tweede orde-zwarte doos

Ik groeide op in een tijd waarin in veel delen van de wereld eindige elementenanalyse (hier ook wel FEA genoemd, een afkorting van het Engelse Finite Element Analysis) op papier werd uitgevoerd. Dat ging als volgt; het onderwerp van deze analyse werd toen handmatig verdeeld in elementen, daarna werden de belangrijkste differentiaalvergelijkingen gelineariseerd en gediscretiseerd in zogenaamde verschilvergelijkingen, vervolgens werden de stijfheidsmatrices op werkbladen opgeschreven en uiteindelijk werd het systeem van vergelijkingen handmatig opgelost. Deze FEA-analyse was meestal lineair elastisch en zeer simplistisch, wat zo zijn nadelen kende, maar het goede aan die tijd was dat het oplossen van een FEA als een glazen doos was. Men kon eenvoudig bepalen op welke manier en met welke methoden de ingevoerde gegevens omgezet konden worden naar de uitkomst van de vergelijking.
Toen kwam de tijd dat de rekenkracht van computers begon toe te nemen. Onderzoekers begonnen programma’s te schrijven die in staat waren invoer te lezen, lichamen te meshen, het systeem van vergelijkingen op te stellen en oplossingen te vinden voor lineaire en niet-lineaire problemen. De onderzoekers die toegang hadden tot de broncodes, konden nog steeds de processen begrijpen die aan de back-end aan de gang waren, maar degenen die alleen toegang hadden tot de uitvoerbestanden waren praktisch blind vanuit het FEA-perspectief. Daarna kwam de tijd van commerciële FEA-codes. Bijna alle commerciële FEA-providers hebben inmiddels een GUI ontwikkeld voor zowel voor- als nabewerking en interfaces met CAD-programma’s. Het uitvoeren van een FEA-simulatie werd hierdoor voor gebruikers zeer eenvoudig. De processen aan de back-end waren echter niet zichtbaar voor de meerderheid van de gebruikers. Bedrijven begonnen experts op te leiden die hier verstand van hadden en die wisten welke parameters moesten worden aangepast wanneer een bepaald probleem zich voordeed. Maar zelfs deze personen begrepen de beredenering achter die parameterinstelling niet, noch waarom die instelling van toepassing is in de gegeven omstandigheden. Een FEA-analyse veranderde hierdoor aanzienlijk, tot een soort zwarte doos of black box.

De afgelopen twee tot drie decennia waren een achtbaan wat FEA-innovaties betreft. Slimme ideeën waren overal te vinden, en dus ook in de wereld van de berekeningen. Inmiddels zijn er veel slimme trucs gevonden om de rekentijd bij dit soort simulaties aanzienlijk kunnen verkorten. De gesimuleerde problemen worden echter ook steeds complexer, en de rekenkracht voor simulaties is daarom relatief gezien nog steeds beperkt. Om dit te verhelpen, kwam iemand met een heel slim idee, waardoor de fysica uit de zwarte doos van FEA verwijderd kon worden. Als men voldoende input- en outputgegevens uit experimenten (of FEA-simulaties) kan verkrijgen, kan men het fysieke proces nabootsen met behulp van statistische modellen voor bijvoorbeeld de meeste op waarschijnlijkheid gebaseerde neurale netwerken. Dus het nabootsen van het fysieke proces, ofwel het besturen van vergelijkingen met kunstmatige intelligentie (of machine learning-algoritmen), voegt een zwarte doos toe binnen een zwarte doos. Oftewel een tweede orde van onzichtbaarheid voor de gebruiker.
De vraag is nu: “Maakt het echt uit of machine learning-algoritmen een black box zijn?”. Het eerste antwoord is “NEE”, totdat je een situatie bereikt waarin het er wel toe doet. Daarom is het definiëren van de reikwijdte van de inputs van de black box zeer belangrijk. Het is de verantwoordelijkheid van de ontwikkelaar van het machine learning-algoritme om dit bereik te identificeren voor ieder model. Dit betekent dat begrip van de fysica en fenomenen die in de back-end plaatsvinden belangrijk is. Als er niet-lineairheden of discontinuïteiten in het systeem zitten die niet worden geïdentificeerd binnen de verstrekte gegevens, kan het gebruik van het machine learning-algoritme uiterst gevaarlijk zijn. Het is niet alleen belangrijk om deze discontinuïteiten te identificeren, maar ook de volgorde van discontinuïteit (of continuïteit) moet herkend worden. De meeste ontwikkelaars van machine learning-algoritmen zijn echter gegevenswetenschappers die al dan niet de fysica begrijpen waaruit de gegevens worden gegenereerd. De oplossing is om ofwel een data scientist te krijgen die ook de fysica van het proces begrijpt, OF de data scientist samen met fysicus te laten werken zodat de juiste scope en toepasbaarheid van het model gedefinieerd kunnen worden.
Om dit punt te bewijzen, nemen we een holle bol die is geladen met interne druk (als voorbeeld). Laten we, zonder ons al druk te maken over de natuurkundige verschijnselen, beginnen met het laden van de bol met druk en de uitzetting meten. Dan vinden we de straal van de nieuwe, opgerekte bol.
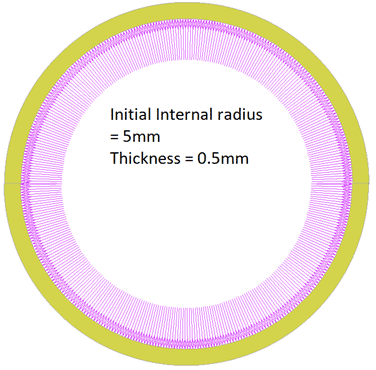
De meetgegevens zijn verzameld tot een druk van 42MPa en worden hieronder weergegeven:
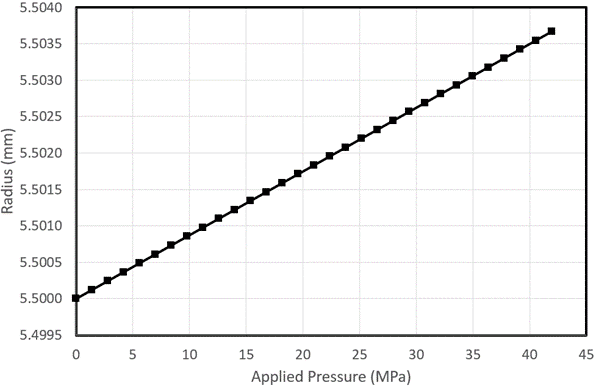
Er is in deze gegevens een duidelijke lineaire trend te zien. Als we nu voorspellingen willen doen op 50MPa, kunnen we dit proberen door dit model lineair te extrapoleren. De verwachte straal van de bol bij 50MPa moet dan 5,5045 mm zijn. Wat we echter in werkelijkheid krijgen, is een straal van 5.511mm bij 50MPa, zoals hieronder getoond:
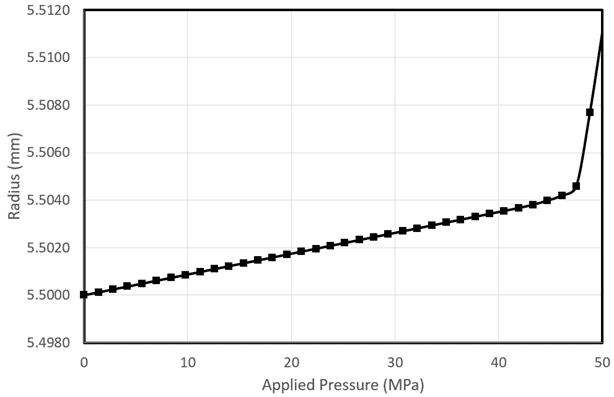
De modelresultaten zijn dus heel nauwkeurig tot ~ 46MPa, maar zodra de druk iets boven 46 MPa gaat, verslechtert de nauwkeurigheid aanzienlijk. Dit komt door een discontinuïteit die bij deze druk zichtbaar wordt.
Laten we dan zeggen dat het doel van het machine learning-model niet is om te extrapoleren, maar alleen om te interpoleren. Om dit te bereiken, kunnen we gegevens verzamelen tot een hoger drukbereik. Het verzamelen van gegevens is echter duur, dus beginnen we met tien datapunten. Hieruit krijgen we de volgende gegevens:
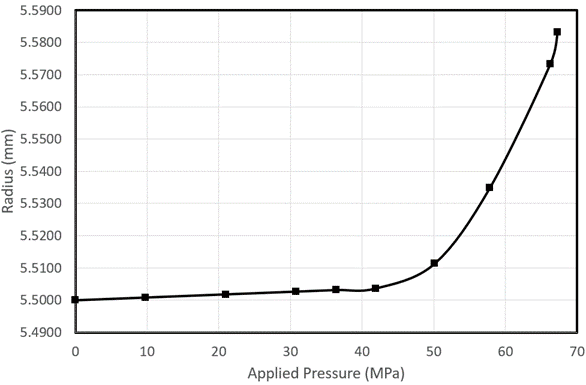
We zien dat deze getallen niet meer lineair zijn tussen ~ 37MPa en ~ 58MPa. Daarnaast zijn we niet zeker over het gedrag tussen 58MPa en 67Mpa. Deze meetwaarden lijken lineair te zijn, maar we hebben geen gegevenspunt ertussen, dus dit bereik kan net zo goed niet-lineair zijn. We voegen meer punten toe tussen 37MPa en 50MPa om de sterke niet-lineariteit te verhelpen, en we doen hetzelfde tussen 50 en 67Mpa voor de zwakke niet-lineariteit die hier te vinden is.
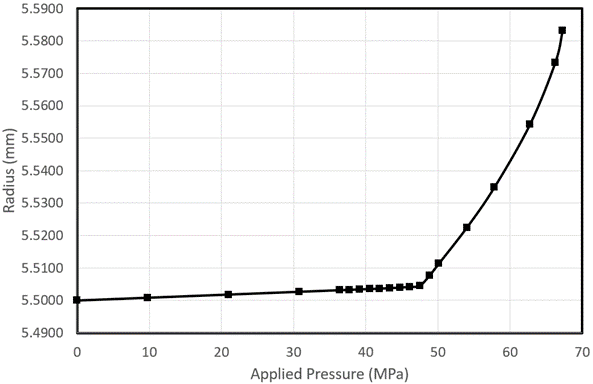
Het toevoegen van meer punten tussen 37MPa en 46MPa, biedt niet veel verbeteringen voor dit model, behalve dat het laat zien dat het model lineair is tussen 0 en 46Mpa en er vervolgens een discontinuïteit en zwakke niet-lineariteit zichtbaar wordt tot ongeveer 63MPa. Als dit vanaf het begin bekend zou zijn geweest, had men veel dure gegevensverzameling niet hoeven uit te voeren. Het model is nu vrij nauwkeurig, maar heeft veel tijd en geld gekost. Het vanaf het begin meenemen van natuurkundige kennis (in dit geval elastische vervorming die verandert in plastische vervorming – en het verhardingsgedrag van materiaal) had de ontwikkeling van machine learning-algoritmen veel nauwkeuriger en goedkoper kunnen maken.

