Machine Learning in FEA: A second order black box

I grew up in an age where finite element analysis was performed on paper, in many parts of the world. The subject matter was manually divided into elements, the governing differential equations were linearized and discretized into difference equations, the stiffness matrices were written down on sheets and the system of equations were solved manually. Indeed, these FEA analysis were mostly linear elastic and very simplistic. But the good thing about that time was that solving an FEA was like a glass box. One can easily determine how the inputs are converted into output.

Then the time came when computational power of computers started increasing. Researchers started writing programs to read inputs, mesh the bodies, develop the system of equations, and find solutions for linear as well as nonlinear problems. The researchers who had access to the source codes can still understand the processes going on at the backend but the ones who had only access to the executables were blind from the FEA processing point of view. Then came the time of commercial FEA codes. Almost all of the commercial FEA providers has a GUI for pre and post processing and interfaces with CAD programs. Running an FEA simulation became very easy from user point of view. However, the processes on the backend were not visible for majority of the users. The companies started developing experts of commercial codes, who knew which parameters to tweak when a problem arises but did not understand the phenomenon behind those parameter settings and if those setting are really applicable in the given conditions. An FEA analysis turned significantly into a black box.

The last two to three decades have been a roller coaster in terms of innovations. Smart ideas can be found everywhere. The same is true in the world of computation. Many smart computational tricks have been employed to reduce the computational time. However, the problems keep getting more and more complex and the computational power for a simulation is still limited. So, someone came up with a very smart idea to eliminate the physics from the black box of FEA. If one can obtain sufficient input and output data from experiments (or FEA simulations) then one can mimic the physical process using statistical models for e.g. most probability based neural networks. So mimicking the physical process/governing equations with artificial intelligence (or machine learning algorithms) adds a black box within a black box i.e. 2nd order invisibility for the user.

The question is “does it really matter if machine learning algorithms are a black box?”. The quick answer is NO, until you reach a situation where it does matter. Therefore, defining the scope of the inputs towards the black box is of prime importance. It is the responsibility of the machine learning algorithm developer to identify the range of validity of the model. This means that understanding of the physics/phenomenon on the backend is also important. If there are any nonlinearities or discontinues in the system which are not identified by the provided data, then usage of the machine learning algorithm can prove extremely dangerous. It is not only important to identify the discontinuities but even the order of discontinuity (or continuity). However, most machine learning algorithm developers are data scientists, which may or may not understand the physics from which the data is generated. The solution is to either get a data scientist who also understands the physics of the process OR make the data scientist work in tandem with physicist so that the proper scope and applicability of the model can be defined.

To prove this point, lets take an example of a hollow sphere which is loaded with internal pressure. Without thinking of the physics, lets start loading the sphere with pressure and measure the expansion i.e. new radius of the sphere.

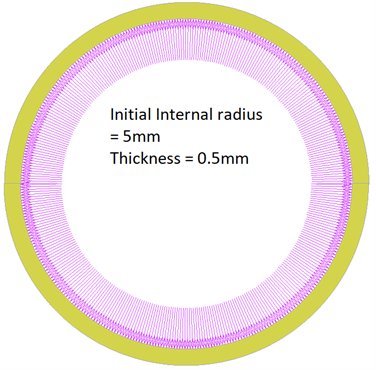
The data was collected up to 42MPa pressure which is shown below:

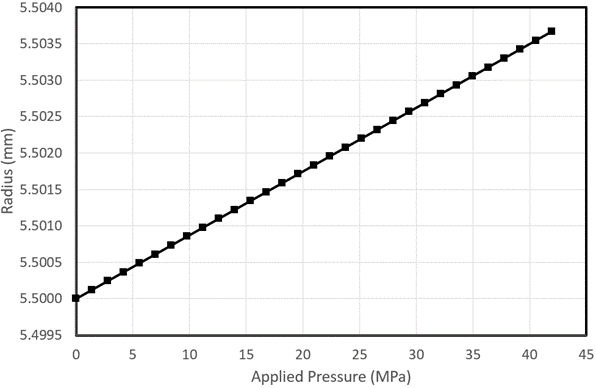
A linear trend can be observed clearly. Now if we want to make prediction at 50MPa, we need to extrapolate this model linearly. The expected radius of the sphere at 50MPa shall be 5.5045mm. But what we get in reality is a radius of 5.511mm at 50MPa as shown below:

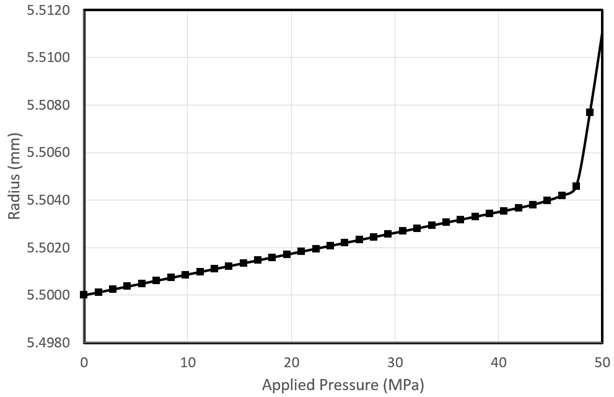
So, the model results are extremely accurate up to ~46MPa but as soon as the pressure goes slightly above 46MPa the accuracy deteriorates significantly. This is due to the discontinuity at this pressure.

Ok let’s say that the scope of the machine learning model is not to extrapolate but only to interpolate. We can collect data to a higher pressure range. However, collecting data is expensive. So we start with 10 data points. We get the following data fit:

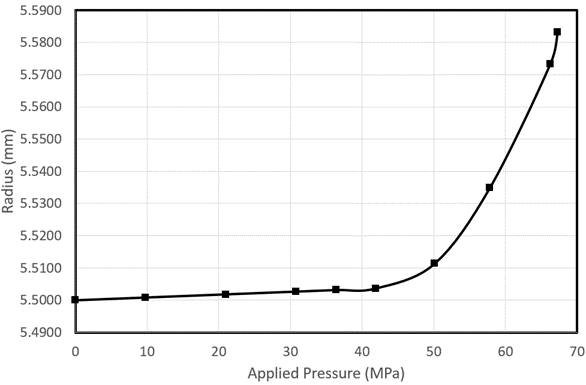
We see that there is nonlinearity starting from ~37MPa up to ~58MPa. We are not sure about the behaviour between 58MPa and 67Mpa. It apparently shows linear behaviour, but we don’t have a data point in between, so it can also be nonlinear. We add more point between 37MPa and 50MPa to cover the strong nonlinearity and a few points between 50 and 67Mpa to cover the weak nonlinearity.

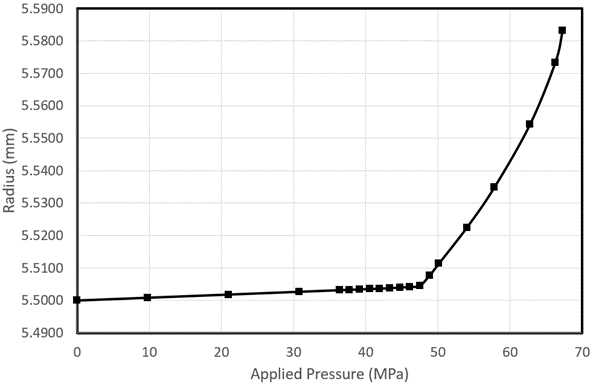
However, adding more points between 37MPa and 46MPa do not add too much to the model except for it shows that the model is linear between 0 and 46Mpa and then there is a discontinuity with weak nonlinearity till 63MPa. If this would have been known from the start, then one could have saved a lot of expensive data collection. The model is now quite accurate, but it cost much more. Bringing in knowledge of physics from the start (in this case elastic deformation changing to plastic deformation and the hardening behaviour of material) could have made the machine learning algorithm development much more accurate and cost effective.